Reciclando papel con 4to E.P

Paenza Maestro!!

http://www.pagina12.com.ar/diario/sociedad/3-253678-2014-08-24.html


Es largo pero vale la pena!

CRIBA DE ERATÓSTENES

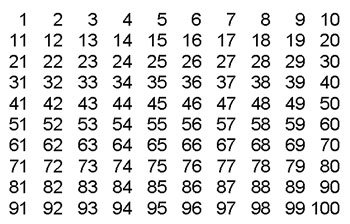
1) Averiguo quién fue Eratóstenes
2)Uso la tabla de arriba para confeccionar una Criba de Eratóstenes
3) La puedo buscar e imprimir o la armo en hoja cuadriculada

CÁLCULO DEL MÁXIMO COMÚN DIVISOR (MCD)

Tarea semanal para 6to

Imprimo la tarea, la resuelvo y entrego con nombre el miércoles 19 de agosto.

Estudio para poder resolver los ejercicios. Recuerdo que la calculadora ya es una herramienta más de las tareas de matemática.

EJEMPLO: Calcular el MCD entre 120 y 144   


Primero descompongo (o "factorizo") los números en sus factores primos

¿Qué son los números primos?: Son los números que sólo son divisibles por sí mismos o por el número 1. Por ejemplo: 7 es un número primo. Porque sólo se puede dividir (división exacta) por 7 o por 1. En su "descomposición" sólo están el 7 y el 1. 7 | 7 1 | 1 Lo mismo pasa con los número 2, 3, 5, 11, 13, 17, 19, etc.  Precisamente, ésos son los números que puedo poner en la columna derecha cuando descompongo un número. No puedo poner 4, 6, 8, 9, 10, etc., porque no son números primos. A los números que no son primos se los llama "compuestos" (exceptuando el 1 y 0, que no son primos ni compuestos). En su descomposición aparecen otros números menores a ellos.

120 | 2               144 | 2
  60 | 2                 72 | 2
  30 | 2                 36 | 2
  15 | 3                 18 | 2
    5 | 5                    9 | 3
    1 | 1                    3 | 3
              1 | 1       

  

¿Cómo se descomponen los números?  Por ejemplo, el 120. Busco el número "más chico" que divida a 120 Resulta ser el número 2. Pongo 2 en la columna derecha, y luego divido 120 : 2 = 60. Y pongo 60 en la siguiente fila a la izquierda. Así: 120 | 2  60 | 2 Ahora busco el número más chico que divida a 60. También es el número 2, lo pongo a la derecha del 60. Divido 60 : 2 = 30, o sea que pongo 30 en la siguiente fila, bajo el 60. Así: 120 | 2  60 | 2  30 | 2 Luego sigo haciendo lo mismo, hasta llegar al número 1. 120 | 2  60 | 2  30 | 2  15 | 3   5 | 5   1 | 1 Los números de la columna derecha son los factores primos que forman la descomposición o factorización del número 120. 120 = 2 . 2 . 2 . 3 . 5       Como 2.2.2 es igual a 23 , también podemos decir que la descomposición del 120 es: 120 = 23 . 3 . 5   Lo convertí en una multiplicación de números primos.

120 = 2³.3.5                        144 = 2⁴.3²

Que es lo mismo que:             Que es lo mismo que:       

120 = 2.2.2.3.5                     144 = 2.2.2.2.3.3

Luego, el MCD se calcula multiplicando todos los "factores" que tienen en "común" ambos números (el 2 y el 3 en este caso), con el menor exponente (la  menor cantidad de veces que aparece el factor primo en la columna derecha) 

Como el número 2 está tres veces en el 120, y cuatro veces en el 144, lo pongo elevado a la tercera (porque es la menor cantidad de veces que aparece, o "menor exponente"). Como el 3 está en ambos números, pero una sola vez en el 120 y dos veces en el 144, lo pongo elevado a la uno (o sin elevar), porque es la menor cantidad de veces que aparece.

MCD = 2³.3 = 8.3 = 24 

MCD (120, 144)= 24

1 En esta página pueden practicar un rato:

http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/03/05.htm

2Recuerdo que cuando busco el MCD entre varios números; la respuesta  ES UN NUMERO y no una expresión

En cambio cuando descompongo en números primos un solo número la respuesta que corresponde es:

Una expresión: el producto de los factores primos obtenidos (o la multiplicación de los factores primos)

Recuerdo que “producto” significa multiplicación.

3 Observa la descomposición en producto de factores primos de los siguientes números:

A = 2² x 3 x 5²

 B = 2² x 3 x 5

C = 2³ x 3² x 5² x 7

a) Calcula el valor de cada uno de estos números

A =………..      B =…………    C =……………..

4 Descompone en factores primos:

1400

2560

3475

KAME...KAME...HAAAAAAAA!!!!!

PARA EL QUE NO ESTUDIE LAS TABLAS!!!

El matemático argentino Miguel Walsh, de 26 años, ganó el premio Ramanujan

Si  la matemática fuera como el rock, Srinivasa Ramanujan sería un ídolo de multitudes: a principios del siglo XX, el genio indio redescubrió la matemática occidental, solo y casi sin entrenamiento formal, cuando todavía no tenía 20 años, y luego hizo extraordinarias contribuciones, particularmente en teoría de números. Murió antes de cumplir los 33.

En octubre próximo, un argentino tendrá el orgullo de recibir el premio internacional que lleva su nombre, uno de los más preciados por su contenido simbólico. La distinción, ofrecida por el Centro Internacional de Física Teórica de Trieste, el Departamento de Ciencia y Tecnología del gobierno de la India y la Unión Matemática Internacional, irá este año a Miguel Walsh, que con 26 años se convertirá en el más joven en recibirlo desde que se entrega, hace nueve años.

El premio le llega meses después de haber sido elegido para recibir la beca del Clay Mathematical Institute , una de las más prestigiosas del mundo, y reconoce anualmente a matemáticos sobresalientes de menos de 45 años. En 2007 lo había ganado otro argentino, Jorge Lauret, de la Universidad Nacional de Córdoba y hoy docente de la Facultad de Matemática, Astronomía y Física.

De visita en el país para pasar unos días con su familia, Miguel no quebranta su habitual sobriedad. Como si el honor no fuera algo desusado, se limita a comentar que tanto él como su familia están "muy contentos".

La historia de Walsh (sobrino nieto del escritor, al que no llegó a conocer) tiene todos los condimentos que hacen del backstage de la matemática una trama que deslumbra a los no iniciados. Nació en Almagro, pero más tarde se mudó con su familia a Palermo, donde estudió en la Escuela Argentina Modelo. De esas épocas, se recuerda como un alumno "normal", que no prestaba mucha atención a la dinámica escolar.

"Siempre me gustaron las tareas que tuvieran algún grado de creatividad y en la escuela la matemática era la materia que menos me atraía -cuenta-. Pero tuve la suerte de que cerca del final del secundario me crucé con problemas abiertos que podía entender. Y ahí me di cuenta de que la matemática era algo diametralmente opuesto a lo que yo pensaba que era. Que en realidad había mucho espacio para crear."

El amor a primera vista de Walsh con "la reina de las ciencias" se produjo casi por casualidad, cuando navegando por Internet se encontró con un problema no resuelto. Obtuvo su licenciatura en Matemáticas en la Universidad de Buenos Aires en tres años y medio, y completó su doctorado en dos años y medio, bajo la supervisión de Román Sasyk.

Según Pablo De Nápoli, que fue profesor de Walsh en la UBA, "Miguel fue un estudiante brillante. Vino a una materia de teoría analítica de números, ¡pero sabía más que yo del tema! Cuando terminó, me dijo que quería hacer la tesis de licenciatura sobre eso. Leyó el trabajo por el que [Terence] Tao ganó la medalla Fields, y un día apareció con una tesis ya toda escrita. Muy bien escrita. Incluso con generalizaciones originales de ese trabajo".

Actualmente instalado en la Universidad de Oxford, donde está haciendo un posdoctorado, Walsh comenta que en el país no tuvo muchas posibilidades de intercambiar ideas con otros que estuvieran trabajando en sus áreas de interés. "Afortunadamente -dice-, hoy Internet ofrece fácil acceso a artículos y blogs que ayudan a compensar esta situación para quienes viven en la periferia."

¿Su consejo a otros jóvenes que emprendan el camino de la matemática? "Es importante mantenerse fiel a los problemas que a uno realmente le interesan -dice-. Aunque suena sencillo, sostener esta convicción exigirá trabajar muy duro."

Parece que la matemática nos ayuda mas de lo que pensamos a darnos cuenta que no hay que rendirse...No??

BIENVENIDOS

PROYECTO

BLOG

 Nunca consideres el estudio como una obligación, sino como una oportunidad para penetrar en el bello y maravilloso mundo del saber.                              

A. Einstein

          Bienvenidos

Las seños de matemática,Practica del lenguaje, Cs. Sociales,Naturales y Computación les damos la bienvenida a las familias de los chicos de segundo ciclo.

La etapa en donde comienzan a ser los mas grandes de la escuela. En donde  van avanzando hacia el  final  de la escuela primaria, y en donde queremos que cuenten con todas las herramientas que podamos darles para manejarse lo mas independiente y eficazmente posible en las próximas etapas escolares.

El blog va a ser un espacio de aprendizaje y entretenimiento, para los chicos y los padres.

Les dejamos los objetivos y comenzaremos a usarlo.

OBJETIVOS

*Crear un BLOG del segundo ciclo de primaria del ciclo oficial, administrado por las docentes de las materias: Matemática,Practicas del lenguaje, Ciencias naturales y sociales y computación. En donde se publicaran actividades, documentos, archivos, imágenes, etc. Que se usarán como recurso didáctico y académico para fines pedagógicos de los alumnos de 4°,5° y 6° año del ciclo primario.

(Un recurso didáctico es cualquier material que maestros o alumnos elaboren, seleccionen y utilicen para apoyar los procesos de enseñanza y de aprendizaje).

*Familiarizarnos tanto los docentes como los alumnos y las familias con las TIC (Tecnologías  de Información y Comunicación)

¿Qué es un BLOG?

Un blog, (también se conocen como weblog o bitácora), es un sitio web que recopila cronológicamente textos o artículos de uno o varios autores, apareciendo primero el más reciente. (http://es.wikipedia.org/wiki/Blog).

La administración de un blog académico la realizan los docentes, en este caso creemos que no debemos abrirlo a comentarios, ya que no va a ser un espacio de charla (chat) sino exclusivamente un lugar de consulta de los alumnos y sus familias  alentado por los docentes de acuerdo a los lineamientos didácticos que merezcan determinados temas.

más curiosidades

Las dos rayas = que indican igualdad las empezó a utilizar un matemático inglés llamado Robert Recorde que vivió hace más de cuatrocientos años. En uno de sus libros cuenta que eligió ese signo porque “dos cosas no pueden ser más iguales que dos rectas paralelas”

El símbolo de raíz se empezó a usar en 1525 y apareció por primera vez en un libro alemán de álgebra. Antes, para indicar la raíz de un número se escribía “raíz de …”. Luego, para abreviar, se empezó a poner “r”. Pero si el número era largo, el trazo horizontal de la “r” se alargaba hasta abarcar todas las cifras. Así nació el símbolo de la raíz, como una “r” mal hecha

Curiosidades de la matemática (para charlar en casa)

La Secuencia de Fibonacci 
En la Naturaleza 

Leonardo de Pisa, llamado Fibonacci, autor de una de las más célebres sucesiones –si no la más célebre- de múltiples aplicaciones e invalorable aplicación para la interpretación de distintas manifestaciones de la naturaleza.

Siglo XII. En 1170, los normandos atacan a los irlandeses en Baginbun y los destrozan, mientras Gervasio de Canterbury y los astrónomos chinos documentan un tránsito de Marte frente a Júpiter. El judío sefaradí Benjamín de Tudela viaja por todo el mundo conocido para censar a los judíos existentes, y llega a la conclusión de que 8 millones de ellos están repartidos por el planeta. El Valle del Bekaá es devastado por un espantoso terremoto de más de grado 7 en la Escala de Mercalli. Ricardo Corazón de León, mientras tanto, reina en Inglaterra.

Entre tantos eventos importantes, un tal Bonaccio, residente en Pisa (donde, según Benjamín, vivían 20 judíos) celebra el nacimiento de su hijo Leonardo. Como era vástago de Bonaccio, casi nunca nadie conoció al niño como Leonardo de Pisa, sino como "el hijo de Bonaccio", esto es, Fibonacci.

Bonaccio, por entonces director de una aduana italiana en Argelia, necesita que su hijo sepa de números, por lo que obliga al chiquillo a estudiar aritmética posicional hindú.

 Milagrosamente, Fibonacci descubrió en las matemáticas el amor de su vida. Nunca más las abandonó.

 El aporte de Fibonacci a la matemática es tan grande y tan profundo que prácticamente no puede ser medido. Por la época en la que vivió, el sistema de numeración arábigo era poco menos que una curiosidad: todo el mundo usaba los números romanos. Y ya se sabe lo difícil que es multiplicar por no hablar de dividir con números romanos. Fibonacci, recordando el curso de aritmética hindú aprendido de niño, escribe, en 1202, su tratado Liber abaci ("El Libro del Ábaco") que es, ni más ni menos, un tratado sobre el sistema numeral indo arábigo.  El que usamos ahora.

 En él presenta al público y a los científicos europeos los signos hindúes (1, 2, 3...) y el 0 árabe, donde dice que se llama "cero" (quod arabice zephirum appellatur…Uhhh Latín). Además, expone el método de regula falsi (otra vez latín) para ecuaciones de primer grado. Nada menos que eso, algo insólito para un libro del siglo XIII en una sociedad que no usaba el cero.

 Muchos  conocemos la secuencia de Fibonacci  por haber visto la película del Código DaVinci . Les cuento de qué se trata:   se trata de una progresión numérica en la cual el siguiente número es el resultado de la suma de los dos anteriores (1, 1, 2, 3, 5, 8, 13,...)  Ahora bien, esta secuencia, que al parecer no tiene mucha significancia, posee muchas propiedades interesantes que la hacen un elemento de estudio bastante cultivado, sobretodo por las propiedades matemáticas que presenta. Pero una de los aspectos más relevantes de esta secuencia es que se presenta en nuestro mundo natural, muy a menudo y probablemente sin que nos demos cuenta. 

Veamos algunos ejemplos: 

Si se observa un árbol, en la primera parte hay un tronco, le sigue, en la segunda, una parte más fina, en la tercera, dos ramas, en la cuarta, tres, luego cinco y ¡Fibonacci presente!

Sigo viendo más Fibonacci en: http://www.edutecne.utn.edu.ar/geptecne/03-GEPTECNE.pdf

y

http://www.curiosaweb.com/la-secuencia-de-fibonacci-en-la-naturaleza/

http://www.pagina12.com.ar/diario/ciencia/19-245660-2014-05-07.html

CIENCIA › DIALOGO CON YVES CHEVALLARD, LICENCIADO EN MATEMATICAS E INVESTIGADOR DE LA UNIVERSITE D’AIX-MARSEILLE II

Los números no muerden

En las escuelas las matemáticas se presentan, en general, como un obstáculo que los alumnos deben sortear en forma penosa. Por ello, la propuesta es clara: desmatematizar las matemáticas para acercar los números a la vida cotidiana.http://www.pagina12.com.ar/diario/ciencia/19-245660-2014-05-07.html